TRIGONOMETRÍA MATEMÁTICAS SECUNDARIA BACHILLERATO

TRIGONOMETRÍA, RECURSOS PARA SECUNDARIA Y BACHILLERATO:

ASPECTOS DE TRIGONOMETRÍA BÁSICA DE INTERÉS:

LA SUMA DE LOS TRES ÁNGULOS DE UN TRIÁNGULO CUALQUIERA ES 180º:

Para cualquier triángulo, la suma de sus ángulos es de 180º:

VÍDEO QUE COMPRUEBA ESTA PROPIEDAD: https://youtu.be/n9gP8f3oIXA

CONFIRMACIÓN / DEMOSTRACIÓN DE LOS VALORES DE LAS RAZONES TRIGONOMÉTRICAS DE 30º Y DE 60º; DE MANERA GENERAL Y SIN CALCULADORA:

VÍDEO QUE RESUELVE LA CUESTIÓN PLANTEADA: https://youtu.be/Ky_NK6AWnmg

CONFIRMACIÓN / DEMOSTRACIÓN DE LOS VALORES DE LAS RAZONES TRIGONOMÉTRICAS DE 45º, DE MANERA GENERAL Y SIN CALCULADORA:

VÍDEO QUE RESUELVE LA CUESTIÓN PLANTEADA: https://youtu.be/wePTenISH3I

DEMOSTRACIÓN DE LA RELACIÓN FUNDAMENTAL DE LA TRIGONOMETRÍA:

sen² α + cos² α = 1

VÍDEO QUE RESUELVE LA CUESTIÓN: https://youtu.be/OGWq5nylBNQ

OBTENCIÓN DE LAS EXPRESIONES TRIGONOMÉTRICAS DE INTERÉS:

1 + cotg² α = cosec2 α   ;   tg² α + 1 = sec² α

A PARTIR DE LA RELACIÓN FUNDAMENTAL DE LA TRIGONOMETRÍA:

sen² α + cos² α = 1

VÍDEO QUE OBTIENE LAS EXPRESIONES: https://youtu.be/8LfiGyJMLts

REDUCCIÓN AL PRIMER CUADRANTE: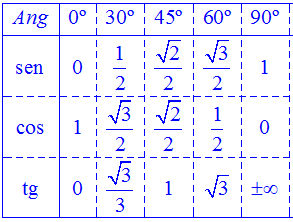

Exclusivamente conociendo las razones trigonométricas de los ángulos fundamentales del primer cuadrante, que deben memorizarse, obtener las siguientes razones trigonométricas, por traslado al primer cuadrante, utilizando razonadamente la circunferencia goniométrica.

EJERCICIO M1BE2103:

a.- cos 210º=

b.- sen 210º=

c.- sen 330º=

d.- cos 330º=

e.- sen 150º=

f.- cos 150º=

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/Cbwal7u9lHE

ENLACES A CONTENIDOS DE TRIGONOMETRÍA:

• Resumen de Fórmulas de prácticamente toda la Trigonometría (128): RESUMEN FÓRMULAS TRIGONOMETRÍA
• Resolución de triángulos rectángulos: TRIÁNGULOS RECTÁNGULOS
• Teorema del Seno, Demostración: DEMOSTRACIÓN TEOREMA SENO
• Teorema del Coseno, Demostración: DEMOSTRACIÓN TEOREMA COSENO
• Teorema de la Tangente, Demostración: DEMOSTRACIÓN TEOREMA TANGENTE
• Resolución de Triángulos cualesquiera, casos y ejercicios: TRIÁNGULOS OBLICUÁNGULOS
• Fórmula de Herón, para cálculo de áreas de un Triángulo cualquiera: FÓRMULA HERÓN: CÁLCULO DEL ÁREA DE UN TRIÁNGULO
• IR A ESTRATEGIAS CONVENIENTES PARA RESOLVER UNA ECUACIÓN TRIGONOMÉTRICA
• Ejercicios con Solución de Ecuaciones Trigonométricas: EJERCICIOS CON SOLUCIÓN DE ECUACIONES TRIGONOMÉTRICAS
  
• PERIODICIDAD DE LAS FUNCIONES TRIGONOMÉTRICAS

• Ejercicios Resueltos de Obtención de Máximos y Mínimos en Funciones Trigonométricas, que suponen un Interesante ejemplo de combinación de Problemas de Optimización con Ecuaciones Trigonométricas:
  

OBTENCIÓN DE MÁXIMOS Y MÍNIMOS EN FUNCIONES TRIGONOMÉTRICAS

• Ejercicios resueltos de simplificación de expresiones Trigonométricas: SIMPLIFICACIÓN EXPRESIONES TRIGONOMÉTRICAS
  
• Ejercicios resueltos de demostración de Identidades Trigonométricas: IDENTIDADES TRIGONOMÉTRICAS
  

• Método de integración de funciones trigonométricas : INTEGRALES TRIGONOMÉTRICAS

Puede interesar ir a RESOLUCIÓN DE ECUACIONES TRIGONOMÉTRICAS

VOLVER A MATEMÁTICAS POR TEMAS

IR A FÍSICA POR TEMAS

IR A QUÍMICA POR TEMAS