POSICIONES RELATIVAS DE DOS RECTAS PARA 2º DE BACHILLERATO.
QUÍMICA BÁSICA, TABLA PERIÓDICA, ESTRUCTURA DEL ÁTOMO, COMPUESTOS, VALENCIA
27 mayo 2020Resolución de los Ejercicios de Discusión de Sistemas de Ecuaciones por Rouché
16 junio 2020POSICIONES RELATIVAS DE DOS RECTAS PARA 2º DE BACHILLERATO.
Mostraremos instrucciones para el estudio de las posiciones relativas de dos rectas en el espacio 3D, que es lo adecuado para 2º de Bachillerato de dos formas: MEDIANTE EL ESTUDIO DE RANGOS y utilización del TEOREMA DE ROUCHÉ; y mediante PUNTOS Y VECTORES. Se considera a este nivel por parte de numerosos profesores mucho más interesante el estudio a través de los rangos, ya que consolida el análisis de los sistemas de ecuaciones y de sus soluciones a través del Teorema de Rouché, con lo cual es una aplicación contextualizada del mismo en la geometría.
ESTUDIO DE LAS POSICIONES RELATIVAS DE DOS RECTAS MEDIANTE RANGOS:
Imaginemos que las dos rectas, r y s, están expresadas en forma paramétrica:
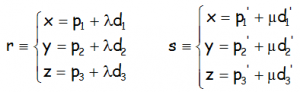
La recta r está determinada por lo tanto por el punto P y el vector d:
P (p1,p2,p3) y d=( d1,d2,d3)
En negrita queremos indicar vector
La recta s está determinada por lo tanto por el punto P’ y el vector d’:
P’ (p’1,p’2,p’3) y d’=( d’1,d’2,d’3)
Como siempre que deseamos estudiar la posición relativa, comparamos las expresiones de lo que queremos comparar a través de un sistema de ecuaciones, y del análisis de sus soluciones sacaremos conclusiones. El sistema más cómodo es el que resulta de igualar las componentes de una y otra recta:
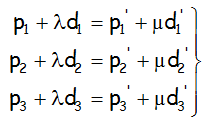
Que arreglando, teniendo en cuenta que sólo nos aparecen los dos parámetros como incógnitas, que ponemos en los miembros de la derecha, ya que todo lo demás son números:
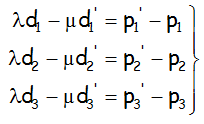
Nos queda, la matriz asociada a este sistema de ecuaciones, donde la matriz M* ampliada es la que se muestra::
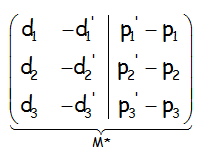
Y la matriz M, de los coeficientes:
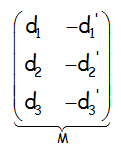
Notar que podemos directamente identificar estas dos matrices, independientemente de que las rectas estén en forma paramétrica, lo que necesitamos es un punto y un vector de cada una de ellas.
Ahora, apoyándonos en las dos matrices y en el Teorema de Rouché, podemos identificar a través de los rangos las distintas posiciones relativas entre dos rectas:
Si el rango de M es 1, significará que los vectores directores son proporcionales, con lo cual las dos rectas son paralelas en sentido general. En sentido estricto:
Si el rango de la matriz ampliada M* es 1, por el Teorema de Rouché, significará que el sistema que tiene sólo dos incógnitas, λ y µ, será compatible indeterminado, infinitas soluciones, las dos rectas comparten infinitos puntos, en consecuencia las RECTAS SON COINCIDENTES
Si el rango de la matriz ampliada M* es 2, por el Teorema de Rouché, significará que el sistema es imcompatible, no tiene solución, las dos rectas no comparten nada, siendo sus directores paralelos, en consecuencia las RECTAS SON PARALELAS EN SENTIDO ESTRICTO.
Si el rango de M es 2, significará que los vectores directores no son proporcionales, con lo cual, se pueden dar dos situaciones en el espacio: que se corten en un punto, o que se crucen sin cortarse.
Si el rango de la matriz ampliada M* es 2, por el Teorema de Rouché, significará que el sistema que tiene sólo dos incógnitas, λ y µ, será compatible determinado, una única solución, las dos rectas comparten un único punto, en consecuencia las RECTAS SON SECANTES, se cortan en un punto.
Si el rango de la matriz ampliada M* es 3, por el Teorema de Rouché, significará que el sistema será incompatible determinado, no tiene solución, las dos rectas no comparten nada, siendo sus directores no paralelos, en consecuencia las RECTAS SE CRUZAN.
EJERCICIO DE ESTUDIO DE POSICIONES RELATIVAS DE DOS RECTAS MEDIANTE RANGOS:
CLASE ON-LINE M2GEO04, EJERCICIO M2BE1958:
Estudiar la posición relativa de las rectas:
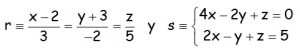
IR AL VIDEO EN FORMATO CLASE QUE RESUELVE EL EJERCICIO, CON EXPLICACIÓN TEÓRICA DEL PROCESO: https://youtu.be/APqCSw2KY40
POSICIONES RELATIVAS DE DOS RECTAS, MEDIANTE EL ANÁLISIS DE SUS PUNTOS Y VECTORES:
Este sistema no es el más recomendable, aunque debido a la inmediatez con la que el alumno desea responder a las preguntas que se le solicitan, quizás alguno lo prefiera. La recomendación es poder trabajar con rangos, para como decíamos, consolidar y combinar contenidos de nivel. En cualquier caso, ambos métodos están relacionados, como podrá observarse, ya que el determinante que resulta al final de este método coincide con el que se genera en la matriz ampliada del método anterior.
Si el vector director de r y el vector director de s son proporcionales, las dos rectas pueden ser paralelas o coincidentes. En este caso, elijo un punto P de r y lo sustituyo en s.
Si ese punto pertenece a s, entonces son coincidentes.
Si no pertenece a s, entonces son paralelas.
Si el vector director de r y el vector director de s no son proporcionales, las dos rectas pueden cortarse en un punto o cruzarse. Elijo en este caso un punto P de r y un punto P’ de s y construyo el vector PP’. Realizo el determinante 3×3 en el que ponto en la primera fila las componentes del director de r, en la segunda fila las componentes del vector de s, y en la tercera fila las componentes del vector PP’. Si el determinante es igual a cero, las rectas se cortan en un punto (ya que en este caso el vector PP’ sería combinación lineal de los dos directores), si es distinto de cero entonces se cruzan.
IR A MÁS RECURSOS Y MATERIALES AUDIOVISUALES DE GEOMETRÍA, DEL PROYECTO DE CIENCIAS ACHIMAGEC: https://achimagec.com/geometria-bachillerato-recursos/
VOLVER A EJERCICIOS Y RECURSOS DE GEOMETRÍA DE BACHILLERATO
IR A GEOMETRÍA
