EJERCICIOS RESUELTOS DE DISCUSIÓN DE SISTEMAS DE ECUACIONES LINEALES POR EL TEOREMA DE ROUCHÉ Y RESOLUCIÓN POR LA  REGLA DE CRAMER, ANALIZANDO EL RANGO DE LAS MATRICES ASOCIADAS, UTILIZANDO DETERMINANTES, PARA MATEMÁTICAS DE BACHILLERATO:

Podría interesar consultar: RANGO DE UNA MATRIZ

Tener en cuenta que para que un sistema sea COMPATIBLE (tenga solución), el rango de la matriz de los coeficientes tiene que coincidir con el rango de la matriz ampliada (incluyendo la columna de los términos independientes); en caso contrario sería INCOMPATIBLE (sin soluciones).

Si además de la coincidencia de rangos entre las matrices de los coeficientes y la ampliada, el rango es igual al número de incógnitas, el sistema sería COMPATIBLE DETERMINADO (tendría una única solución). Si el valor de la coincidencia de rangos es inferior al número de incógnitas, el sistema sería COMPATIBLE INDETERMINADO (tendría infinitas soluciones). En este último caso, la diferencia entre el valor del número de incógnitas y el valor de la coincidencia de rangos nos daría en número de GRADOS DE LIBERTAD de las soluciones del sistema indeterminado.

Lo anterior se conoce como TEOREMA DE ROUCHÉ-FRÖBENIUS

EJERCICIO RESUELTO DE DISCUSIÓN DE SISTEMAS DE ECUACIONES A TRAVÉS DE VIDEO EXPLICATIVO:

EJERCICIO M2BE1961:

a.- Discutir el siguiente sistema de ecuaciones lineales en función de los valores del parámetro k:

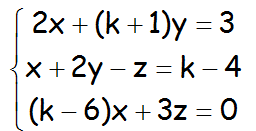
IR AL VIDEO QUE RESUELVE ESTE APARTADO DEL EJERCICIO: https://youtu.be/_DoADYktVXM

b.- Resolver en los casos en que ello sea posible

Si k=5, el sistema es compatible indeterminado, en este caso:

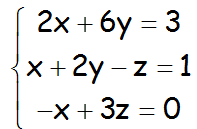
Teniendo en cuenta que el rango tanto de la matriz de los coeficientes, como de la ampliada es igual a 2, nos indica que una de las ecuaciones es combinación de las otras dos (al no haber proporcionalidad entre ninguna de ellas), podemos por lo tanto eliminar cualquiera de ellas (la más complicada -la segunda-) y llamando λ a la incógnita z, nos quedarían las siguientes soluciones:

Si k ≠ 5 y k ≠ -3, el sistema sería compatible determinado, que resolviendo por Cramer y simplificando al máximo:

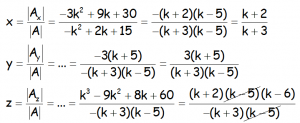
MÁS EJERCICIOS RESUELTOS DE DISCUSIÓN DE SISTEMAS DE ECUACIONES POR EL TEOREMA DE ROUCHÉ Y DE RESOLUCIÓN POR LA REGLA DE CRAMER:

EJERCICIO M2BE75:

  Discutir y resolver según los valores de a el siguiente sistema de ecuaciones lineales:

IR A LA RESOLUCIÓN DE ESTE EJERCICIO

EJERCICIO M2BE1825:

  Dado el sistema:

   Hallar el valor del parámetro a para que sea incompatible. ¿Por qué lo es?

IR A LA RESOLUCIÓN DE ESTE EJERCICIO

VOLVER A ÁLGEBRA LINEAL, MATRICES Y DETERMINANTES

VOLVER A MATEMÁTICAS POR TEMAS

IR A FÍSICA POR TEMAS

IR A QUÍMICA POR TEMAS