Ecuaciones Logarítmicas para Secundaria y Bachillerato
Funciones Hiperbólicas y sus Derivadas para Matemáticas de Bachillerato
3 enero 2013Resolución del Ejercicio de Equilibrio Químico (Cociente de Reacción) para Química de 2º de Bachillerato
13 enero 2013Ecuaciones Logarítmicas para Secundaria y Bachillerato
ECUACIONES LOGARÍTMICAS, PARA MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO: Una ecuación logarítmica es una ecuación en la que la incógnita que tenemos que resolver se encuentra “sometida” a un logaritmo.
Por ejemplo: log (x+3) = 2, o inclusos más complicadas, como la que se muestra, resuelta a través de un video.
Con log se indica el logaritmo en base 10, pero las estrategias que comentamos para las ecuaciones logarítmicas sirven para cualquier base.
EJERCICIO M1BE1962: EJERCICIO RESUELTO A TRAVÉS DE MATERIAL AUDIOVISUAL
Resolver la siguiente ecuación logarítmica:
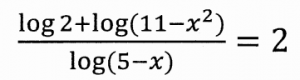
IR AL VIDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/WWC0m8V6ooY
La mejor estrategia para resolver estas ecuaciones logarítmicas, es intentar llevar estas ecuaciones logarítmicas a lo que podemos llamar el “penúltimo paso”, que es:
log A = log B
Evidentemente los logaritmos de cada uno de los miembros tienen que estar en la misma base
Para conseguir que aparezca un único logaritmo en cada miembro de la ecuación (y en los dos miembros), normalmente tenemos que utilizar las PROPIEDADES DE LOS LOGARITMOS; básicamente las siguientes:
O tener en cuenta que por la definición de logaritmo:
Que entre otras cosas implica que:
Podemos transformar fácilmente números cualquiera en logaritmos de otros números:
Por ello podemos decir que 2 = log 100; 3 = log2 8 …
Una vez tenemos con estas estrategias y con las propiedades de los logaritmos, la ecuación transformada a:
log A = log B
Podemos decir que:
A = B
Es decir, podemos PRESCINDIR DE LOS LOGARITMOS, y transformar la ecuación logarítmica en una ecuación normal y corriente, sin logaritmos, una ecuación algebraica cualquiera.
En el EJEMPLO que hemos puesto al comienzo, transformando el número 1 del segundo miembro por el log 10 para tener logaritmos en los dos miembros, podemos prescindir de los logaritmos y tener una ecuación sencilla:
IMPORTANTE:
Cuando resolvemos la ecuación, hay que comprobar las soluciones en la ecuación original, ya que alguna de ellas podría no ser cierta y lo que es peor, alguna de ellas podría dar lugar a que en la ecuación original diera lugar a un logaritmo de un número negativo o de cero, que no existen. Estas soluciones en su caso, se desecharían.
OTRO EJEMPLO, utilizando las propiedades y transformando el número 2 por el log 100:
IR A EJERCICIOS RESUELTOS DE ECUACIONES LOGARÍTMICAS
VOLVER A ARITMÉTICA
VOLVER A ÁLGEBRA
VOLVER A MATEMÁTICAS POR TEMAS
