Matriz Inversa
Álgebra Lineal: Matrices, Determinantes y resolución y discusión de sistemas de ecuaciones.
17 junio 2020Resolución de Ecuaciones Trigonométricas
7 agosto 2020Matriz Inversa
MATRIZ INVERSA. La matriz inversa es la que al multiplicarla con la matriz de la que es inversa, nos devuelve el elemento neutro del producto:
![]()
Si bien la propiedad conmutativa no siempre se cumple en el producto de matrices, sí se cumple en este caso.
Donde la matriz I (identidad), el elemento neutro del producto de matrices:
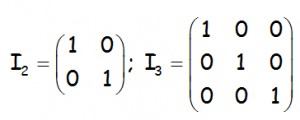
Todos los elementos son nulos, salvo los elementos de la diagonal principal.
Notar como efectivamente, la matriz I, es el elemento neutro del producto de matrices, viendo el siguiente ejemplo de orden 2:
![]()
Si bien la propiedad conmutativa no siempre se cumple en el producto de matrices, sí se cumple en este caso.
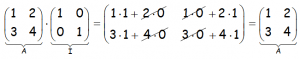
Una matriz cuadrada tiene inversa cuando su determinante es distinto de cero. En este caso se dice que es regular. En este caso, la matriz inversa de A se puede obtener del siguiente modo:
Si A es la matriz:
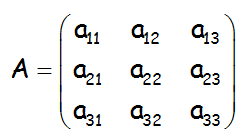
Su inversa será:
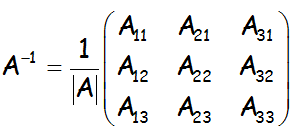
Donde debemos notar que la matriz con la que obtenemos la inversa es la matriz de los adjuntos pero traspuestos: sus elementos son los adjuntos de cada uno de los elementos pero están traspuestos (cambiadas las filas por las columnas).
Operativamente lo conveniente es:
1.- Obtener el determinante. Si es cero, no tiene inversa.
2.- Elaborar la matriz de los menores complementarios de cada elemento (αij)
3.- Cambiar el signo para obtener la matriz de los adjuntos (Aij)
4.- Trasponer esa matriz para obtener la matriz de los adjuntos traspuesta (Aji)
5.- No olvidar dividir cada elemento por el valor del determinante.
EJERCICIO M2BE1959:
a.- Matriz inversa: Definición.
b.- Hallar la matriz inversa de A, siendo A:
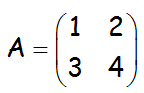
c.- Comprobar que la matriz inversa (A-1) obtenida en el apartado anterior, realmente es la inversa de A, realizando el producto correspondiente.
IR AL VIDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/_zRORL9wjjs
EJERCICIO M2BE1960:
Hallar la matriz inversa de A, siendo A:
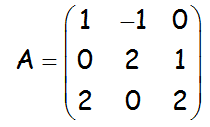
SOLUCIÓN:
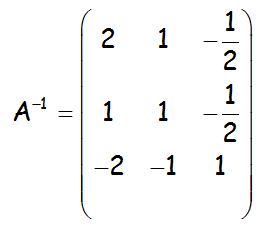
IR AL VIDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/zHNKKOOS3vg
VOLVER A ÁLGEBRA DE MATRICES
VOLVER A MATEMÁTICAS POR TEMAS
IR A FÍSICA POR TEMAS
IR A QUÍMICA POR TEMAS
