Ejercicios de cálculo de parámetros (aplicaciones de la derivada) para matemáticas de 2º de Bachillerato
LEY DE COULOMB, INTENSIDAD DE CAMPO, POTENCIAL Y TRABAJO. ELECTROSTÁTICA, CLASES ONLINE
22 mayo 2020Problemas de Optimización, de Máximos y Mínimos
23 mayo 2020Ejercicios de cálculo de parámetros (aplicaciones de la derivada) para matemáticas de 2º de Bachillerato
CÁLCULO PARÁMETROS MATEMÁTICAS BACHILLERATO
EJERCICIOS CON SOLUCIÓN DE CÁLCULO DE PARÁMETROS DE FUNCIONES DESCONOCIDAS EN APLICACIONES DE LA DERIVADA:
PODRÍA INTERESAR IR A INDICACIONES PARA RESOLVER ESTOS EJERCICIOS DE PARÁMETROS
CLASE ON-LINE M2DER01, donde se resuelve el ejercicio siguiente, en formato clase online*, a través de video.
*Cuando decimos en formato clase online, nos referimos a que se intenta realizar de manera informal, sin revisiones, con la naturalidad de la clase, con los comentarios habituales de una explicación presencial, como si no estuviera grabándose.
EJERCICIO M2BE1521:
Dada la función f(x) = ax2+ bx + c , determinar los valores de a , b y c para que se cumpla: que la gráfica de f(x) pase por el punto (0, 4) y que la recta y = – 4x + 7 sea tangente a la gráfica de f (x) en el punto de abscisa x = 1.
VIDEO DE LA CLASE ONLINE QUE RESUELVE EL EJERCICIO:https://youtu.be/13pDHPgLvtU
IR A OTRO VIDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/hH5gaOV6CrY
EJERCICIO M1BE2027JL:
Determinar los valores de a, b y c sabiendo que la función f(x) = x3+ax2+bx+c , tiene extremos relativos en x=1 y x=-3, y que corta a su función derivada en x=0. Determinar asimismo la naturaleza de los extremos.
IR AL VIDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/UddHOBnzfRU
EJERCICIO M1BE2028JL:
Determinar una función de la forma f(x) = x3+ax2+bx+c ,que tenga un extremo relativo en el punto de abscisa x=2 y para la cual el punto P(1, 2) sea un punto de inflexión.
IR AL VIDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/z5oCkg4bWTQ
EJERCICIO M1BE2029JL:
Se sabe que la gráfica de la función siguiente f(x):
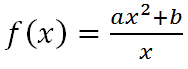
tiene una recta tangente horizontal en el punto P(2, 4). Hallar los valores de a y b.
IR AL VIDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/KVSzz4y0xoQ
EJERCICIO M1BE1953:
Hallar a, b , c, y d para que f(x) = ax3+bx2+cx+d tenga un máximo en M ( 0 ,4 ) y un mínimo en m ( 2, 0).
EJERCICIOS CON SOLUCIÓN DE CÁLCULO DE PARÁMETROS APLICANDO LA DERIVADA:
EJERCICIO M2BE1554:
Se sabe que la gráfica de la función: f(x)=x3+ax2+bx+c, es la que aparece en el dibujo.
a) Determinar la función.
b) Calcular el área encerrada por la función y el eje de las x.
EJERCICIO M2BE1699:
Determinar una función de la forma:
que tenga un extremo relativo (máximo o mínimo) en el punto de abscisa x=2 y para la cual el punto P(1,2) sea un punto de inflexión.
EJERCICIO M2BE1714:
Dada la función:
calcular los valores de a y b sabiendo que la función tiene dos puntos de inflexión, uno en x=1 y otro en x=1/2.
EJERCICIO M2BE1715:
Sea:
un polinomio que cumple f(1)=0, f’(0)=2 y tiene dos extremos relativos para x=1 y x=2.
a) Hallar a, b, c y d
b) ¿Son máximos o mínimos los extremos relativos?
EJERCICIO M2BE1716:
La curva:
corta al eje de abscisas en x=-1 tiene un punto de inflexión en (2,1). Calcula a, b y c.
EJERCICIO M2BE1717:
De la función:
sabemos que pasa por (1,1) y en ese punto tiene tangente paralela a la recta 3x+y=0.
a) Hallar a y b.
b) Determina sus extremos relativos y sus intervalos de crecimiento y decrecimiento.
EJERCICIO M2BE1718:
La función:
verifica que f(1)=1, f’(1)=0 y que f no tiene extremo relativo en x=1. Calcular a, b y c.
EJERCICIO M2BE1719:
Sea:
Hallar a y b para que la curva y=f(x) tenga en x=1 un punto de inflexión con tangente horizontal.
EJERCICIO M2BE1720:
La curva:
corta al eje OX en x=1 y tiene un punto de inflexión en (3,2). Calcular los puntos de la curva que tengan recta tangente al eje OX.
IR A LAS SOLUCIONES DE ESTOS ÚLTIMOS EJERCICIOS DE OBTENCIÓN DE PARÁMETROS
VOLVER A ANÁLISIS DE FUNCIONES
VOLVER A MATEMÁTICAS POR TEMAS
IR A FÍSICA POR TEMAS
IR A QUÍMICA POR TEMAS
